| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
- python #pandas #data_preprocessing #data_process
- 특정값지우기
- git
- SQL #PostgreSQL
- 시계열데이터
- AI #RNN #LSTM #LSTMP #인공지능 #언어학습 #순차학습
- 비동기모듈
- REST_API
- mnist
- SQL #python #MySQL #PostgreSQL
- 깃허브
- 깃
- 판다스 #Pandas #DataFrame #Statistics #통계 #파이썬 #Python #Resample
- aiohttp
- 파이썬
- 선형회귀
- version_error
- Asyncio
- TensorFlow
- ngrok
- pandas #python #date #datetime
- Github
- AI #Inductive_Bias #Relational_inductive_bias
- tf.where
- pandas #python #excel #판다스 #파이썬 #엑셀저장 #xlsxwriter
- Python
- fashionmnist
- pandas #ewma #python #지수이동가중평균 #파이썬 #판다스 #ema #ewm
- MachineLearning
- tensorflow #tensorflow-gpu #python #ubuntu #텐서플로우
- Today
- Total
린스토리
[단순선형회귀] 시계열 데이터 1d Linear Regression으로 값 예측하기 본문
1d 선형식은
y = wx + b의 구조를 가지고 있다.
시계열 데이터에 대입하면, x는 시간 y는 시간에 대응하는 값이 될 것이다. (예시: 주가예측)
오늘은 1d Linear Regression을 간단하게 python으로 코드를 짜볼 것이다.
나는 이 Linear Regression을 x값 중간에 비어있는 시간에 대해 y값을 예측하는 용으로 사용했다.
데이터 구조 파악
우선 데이터의 구조를 보자.
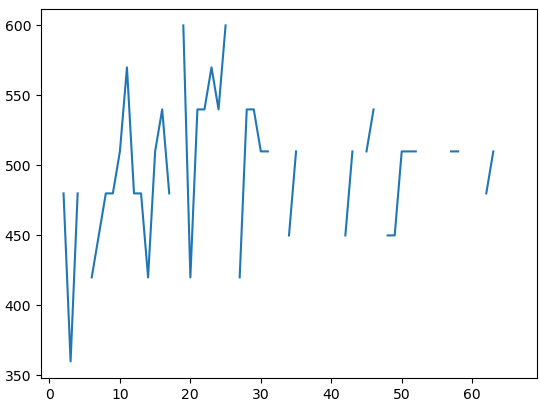

x는 시간이고, y는 실제값이다. 보면 중간 중간 끊겨있는 걸 확인할 수 있다.
이런 빈 값을 linear regression을 통해 채워주려고 한다.
데이터 가공
x는 시간 값이다. 위 그래프에서는 시간으로 표현하지 않았지만, 실제로는 시간의 흐름에 따른 데이터를 보여준다.
이 데이터에 linear regression을 적용하면 어떤 그래프가 나오는지 확인해보자.
import pandas as pd
import matplotlib.pyplot as plt
original_data = pd.read_csv('test.csv')
data = original_data[['test']]
data = data.fillna(0)
# 시간으로 되어있던 X의 범위를 -5~5의 균일한 값으로 변경
x_min = -5
x_max = 5
coeff = (x_max-x_min) / len(data)
new_x = [float(x_min + (coeff*idx)) for idx in range(len(data))]
# train 데이터: None값이 아닌 시간에 대한 값
x_train = [float(x_min + (coeff*idx)) for idx in range(len(data)) if data[idx] != 0]
y_train = [j for j in data if j != 0]
# test 데이터: None값으로, 채워야 하는 값
x_test = [float(x_min + (coeff*idx)) for idx in range(len(data)) if data[idx] == 0]
# None값이 아닌 값에 대해선 원래 y값을 가져와야 하므로 dictionary로 관리
predict_dict = {x: 0 for x in new_x}
for idx in range(len(x_train)):
predict_dict[x_train[idx]] = y_train[idx]Linear Regression for Sequential data of 1D
Linear Regression은 데이터를 선형적으로 매칭시키는 최적의 W(weight)와 B(bias)를 찾는 것이다.
- cost function은 MSE(Mean Squared Error)를 적용하였다.
- gradient는 미분식을 그대로 적용했다.
- 프레임워크를 사용하지 않고 적용하는 것이기에 처음부터 과정을 모두 직접 설계하고 구현해야 한다.
- epoch은 2000번으로 설정하고, learning rate은 0.01로 설정했다.
이 값들 모두 커스터마이징하면 된다.
def linear_regression(X, Y, epochs=2000, learning_rate=0.01):
x_train = np.array(X)
y_train = np.array(Y)
#Initialization
weight = 0.0
bias = 0.0
n_data = len(x_train)
for i in range(epochs):
predicted = x_train*weight + bias
cost = np.sum((predicted - y_train) ** 2) / n_data
gradient_w = np.sum((weight * x_train - y_train + bias) * 2 * x_train) / n_data
gradient_b = np.sum((weight * x_train - y_train + bias) * 2) / n_data
weight -= learning_rate * gradient_w
bias -= learning_rate * gradient_b
if i % 100 == 0:
print('Epoch ({:10d}/{:10d}) cost: {:10f}, W: {:10f}, b:{:10f}'.format(i, epochs, cost, weight, bias))
print('W: {:10f}'.format(weight))
print('b: {:10f}'.format(bias))
print('result : ')
print(x_train * weight + bias)
return weight, bias
Application
None값인 값을 예측하고자 했으므로, 아래와 같이 test를 하여 빈 값 예측 결과를 확인한다.
predicted_weight, predicted_bias = linear_regression(x_train, y_train)
for i in x_test:
predicted_value = round(i * predicted_weight + predicted_bias, 1)
predict_dict[i] = abs(predicted_value)
Visualization
원래의 original data와 linear regression을 통해 빈 값을 채운 결과를 확인하면 다음과 같다.


이렇게 빈값을 간단하게 채워보았다.
다른 방식으로 데이터를 증강하는 법을 구현해보아야겠다.
